این نسخه مناسب است برای: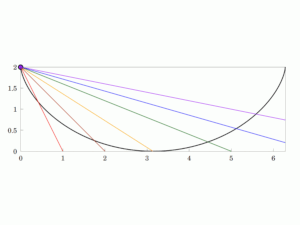
• وزارتخانهها و نهادهای اجرایی
• پژوهشگاهها و مخاطبان غیرریاضی
• ارائهٔ مدیریتی و سیاستگذاری
• نسخهٔ عمومی کتاب SETonic
• ارائهٔ کنفرانسی
بازسازی فرمول و مسئلهٔ براتیستوکرون تحت نظریهٔ تحول سیستمی
________________________________________
✦ چکیده
مسئلهٔ کلاسیک براتیستوکرون منحنیای را تعیین میکند که یک جسم را در کمترین زمان ممکن از نقطهٔ آغازین به نقطهٔ پایانی میرساند. این مسئله بر مبنای مفهوم زمان خطی و گرانش ثابت تعریف شده است. با این حال، در اغلب سیستمهای پیچیدهٔ دنیای واقعی:
• زمان ثابت و یکنواخت نیست
• ساختار سیستم در حال تغییر است
• رفتارها و تصمیمها جریان تحول را عوض میکنند
• اطلاعات، فشار، تنش و جریانهایی وجود دارند که مانند «نیرو» عمل میکنند
نظریهٔ تحول سیستمی (SET) مفهوم تازهای از زمان را مطرح میکند؛ Δτ یعنی «زمان مؤثر تحول». در این نگاه، زمان نه یک ظرف ثابت، بلکه بخشی از خود سیستم است و با تحول سیستم تغییر میکند.
در این مقاله نشان میدهیم که چگونه میتوان مسئلهٔ براتیستوکرون را از حالت کلاسیک به یک مسئلهٔ تحول سیستمی تعمیم داد؛ یعنی پیدا کردن مسیر کمترین زمان مؤثر (Δτ) برای عبور سیستم از وضعیت الف به وضعیت ب. این مسیر، تابعی از ساختار، رفتار، فشار، جریان، شتاب و مومنتوم سیستمی است.
نتیجهٔ کار یک منحنی تحول سیستمی است که مشابه سیکلوئید، اما بسیار پیچیدهتر و واقعگراتر است و میتواند تحول در فیزیک، اقتصاد، هوش مصنوعی، حکمرانی، زیست و سازمانها را توصیف کند.
________________________________________
✦ ۱. مقدمه
براتیستوکرون یکی از مسائل مشهور فیزیک است که به دنبال سریعترین مسیر حرکت در یک میدان ساده است. اما دنیای واقعی چنین نیست:
• سیستمها چندلایه هستند
• زمان برای همهٔ بخشهای سیستم یکسان عمل نمیکند
• ساختارها تغییر میکنند
• فشارها و ریسکها رفتار سیستم را عوض میکنند
• اطلاعات و جریانها باعث انحراف مسیر میشوند
• فازهای تحول (رشد، فروپاشی، گذار) دائماً تغییر میکنند
در نظریهٔ SET، این سیستمها در فضایی حرکت میکنند که «زمان» به صورت یک موجودیت زنده رفتار میکند. هر تغییر در ساختار، رفتار، جریان یا فشار، زمان مؤثر تحول را تغییر میدهد. بنابراین، مسئلهٔ اصلی این میشود:
سیستم چگونه میتواند سریعترین مسیر تحول را طی کند؟
این همان نسخهٔ SET از مسئلهٔ براتیستوکرون است.
________________________________________
✦ ۲. زمان مؤثر — Δτ
در SET، زمان همان زمان فیزیکی نیست. Δτ زمانی است که سیستم واقعاً برای تحول نیاز دارد، نه زمانی که ساعت نشان میدهد.
به عنوان مثال:
• یک سازمان ممکن است در مدت کوتاه فیزیکی، عملاً هیچ تحولی نکند (Δτ بزرگ).
• یک بازار مالی ممکن است در چند دقیقه دچار جهش ساختاری شود (Δτ کوچک).
• یک موجود زنده ممکن است در شرایط خطر، زمان را فشرده تجربه کند (Δτ کوچک).
بنابراین:
مسیر بهینهٔ تحول، مسیری است که کمترین Δτ را مصرف کند.
این مسیر لزوماً کوتاهترین، سادهترین و خطیترین مسیر نیست.
________________________________________
✦ ۳. گرانش سیستمی — نیروی محرک تحول
در فیزیک، گرانش تعیینکنندهٔ شکل منحنی براتیستوکرون است.
در SET، گرانش واقعی وجود ندارد، اما چیزی مشابه و بسیار دقیقتر داریم:
میدان گرانش سیستمی = عواملی که سیستم را به سمت سریعترین تحول میکِشند.
این عوامل شامل:
• فشار سیستمی (تنش، بحران، Bottleneck)
• جریان اطلاعات (Data Flow)
• تغییر ساختار (Structural Evolution)
• رفتارهای شتابدار (Behavioral Momentum)
• سرعت تحول درونی (Δv)
به عبارت دیگر:
سیستم توسط نیروهایی از جنس اطلاعات، ساختار، رفتار و فشار «کشیده» میشود، نه توسط جرم و گرانش.
این میدان، مسیر منحنی تحول را تعیین میکند.
________________________________________
✦ ۴. مفهوم منحنی تحول سیستمی (STC)
منحنی تحول سیستمی، تعمیم یافتهٔ سیکلوئید است.
این منحنی خصوصیات زیر را دارد:
● مسیر همیشه مستقیم نیست
گاهی مسیرهای غیرمستقیم سریعتر هستند.
● رفتار سیستم در طول مسیر تغییر میکند
مثلاً سیستم ممکن است:
• فاز یادگیری
• فاز پرش ساختاری
• فاز تثبیت
• فاز واگشتی
را پشت سر بگذارد.
● فشار و اطلاعات مانند «نیرو» عمل میکنند
سیستمها در حضور اطلاعات قوی یا فشار بالا، مسیرهای کوتاهتری میپیمایند.
● منحنی در فضاهای چندبعدی شکل میگیرد
این فضا شامل Δτ، ساختار، رفتار، جریان و تنش است.
________________________________________
✦ ۵. نسخهٔ سادهشده از کاربردهای اصلی
۵.۱ فیزیک
• تحلیل سیستمهایی که زمان در آنها کش میآید یا فشرده میشود.
• مدلسازی تحول در محیطهای ناپایدار.
۵.۲ زیست و تکامل
• مسیر کمترین زمان برای سازگاری یا دگرگونی.
• شناخت اینکه چرا بعضی جهشها سریع و بعضی کند هستند.
۵.۳ هوش مصنوعی
• تعریف کوتاهترین مسیر یادگیری یک مدل.
• بهبود سرعت یادگیری شبکههای عمیق.
• تولید الگوریتمهای جدید (Brachisto-Optimizer).
۵.۴ اقتصاد و بازارهای مالی (TacZi)
• کوتاهترین مسیر رسیدن از «آشفتگی» به «تعادل»
• یافتن سریعترین مسیر رشد یا ریزش
• تحلیل رفتار معاملهگران به عنوان «میدان فشار»
۵.۵ مدیریت و حکمرانی
• مدلسازی مسیر کمترین زمان برای اصلاحات
• بهینهسازی مسیر تحول اداری
• تشخیص گلوگاهها بر اساس Δτ
۵.۶ سازمانها و کسبوکار
• کوتاهترین مسیر تحول سازمانی
• کاهش زمان تغییر ساختار
• تحلیل Bottleneckها به عنوان موانع براتیستوکرون
۵.۷ جامعهشناسی و رفتار جمعی
• مسیر کمترین زمان برای تغییرات اجتماعی
• تشخیص بحران قبل از وقوع
• تحلیل ورود/خروج جمعیت از فازهای بحرانی
________________________________________
✦ ۶. چارچوب محاسباتی غیرریاضی (نسخهٔ عمومی)
برای شبیهسازی براتیستوکرون سیستمی، کافی است:
1. وضعیت جاری سیستم را مشخص کنیم.
2. عامل یا عوامل فشار را شناسایی کنیم.
3. مسیرهای مختلف تحول را تولید کنیم.
4. زمان مؤثر هر مسیر (Δτ) را اندازه بگیریم.
5. مسیری را انتخاب کنیم که Δτ کمتری دارد.
این چارچوب میتواند در Python/Julia برای نسخهٔ علمی پیادهسازی شود.
________________________________________
✦ ۷. بحث
تحلیل نشان میدهد:
• سیستمها در دنیای واقعی به دنبال کمترین زمان مؤثر تحول هستند، نه کمترین انرژی یا کمترین فاصله.
• مسیر مستقیم معمولاً سریعترین مسیر نیست.
• رفتار جمعی، ساختارهای اجتماعی، بازارها و موجودات زنده همه تابع این اصل هستند.
• براتیستوکرون کلاسیک تنها یک حالت ساده از این مفهوم است.
• نظریهٔ SET امکان مدلسازی مسیرهای تحول را در سیستمهای بسیار پیچیده فراهم میکند.
________________________________________
✦ ۸. نتیجهگیری
در این مقاله یک تعمیم دقیق و جدید از مسئلهٔ براتیستوکرون ارائه شد که در آن:
• زمان تبدیل به زمان مؤثر تحول (Δτ) میشود
• گرانش تبدیل به فشار و میدان سیستمی میشود
• مسیر حرکت تبدیل به مسیر تحول میشود
• شکل سیکلوئید تبدیل به منحنی تحول سیستمی میشود
این چارچوب میتواند بهصورت گسترده در فیزیک، زیست، اقتصاد، هوش مصنوعی، مدیریت و علوم اجتماعی مورد استفاده قرار گیرد.
________________________________________
✦ ۹. مسیرهای آیندهٔ پژوهش
• توسعهٔ هندسهٔ SETonic برای نمایش منحنیهای تحول
• گسترش مدل به فضای چندفازی
• مدلسازی بحرانها بهعنوان نقاط تکینگی Δτ
• استفاده در هوش مصنوعی TacZi و STTI
• ورود به کنترل بهینه در نظریهٔ SET (فصل ۱۵)
