جزوه مقدماتی نظریه SETon و عملگرها

۱. مقدمه

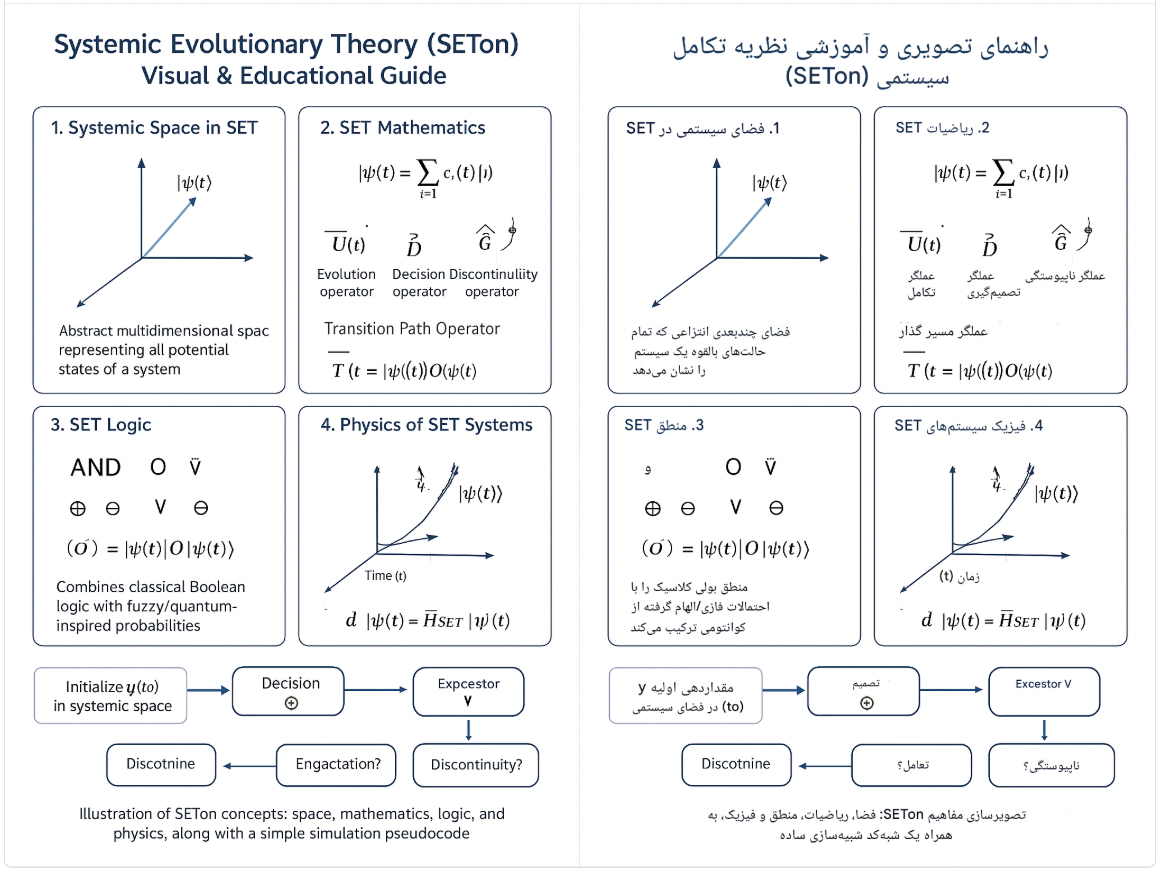
نظریه‌ی SETon (Systemic Evolutionary Theory – Ontological Extension)، توسعه‌ای بر نظریه SET است که به تحلیل سیستم‌های دینامیکی چندزمانه و چندسطحی می‌پردازد. در این چارچوب، فضای کوانتومی-سیستمی جایگزین فضای کلاسیک می‌شود و رفتار سیستم‌ها از طریق عملگرها و رابطه‌های ریاضی حاکم مدل‌سازی می‌شود.

این نظریه تلاش می‌کند:

• تعامل بین زمان‌های درونی و بیرونی سیستم‌ها را مدل کند.
• گسست‌ها، گذارها و آشوب‌ها را به شکلی ریاضیاتی و فیزیکی تحلیل نماید.
• چارچوبی مبنایی و منطقی برای توسعه مدل‌های پیش‌بینی و تحلیلی ارائه دهد.

\(\; \)

۲. فضای حاکم SETon

۲.۱ تعریف فضا

فضای \( SETon \) به‌صورت یک فضای چندبعدی دینامیکی تعریف می‌شود که در آن:

 \[ SETon={x_i,t_j,ψ_k \hspace{10pt}∣\hspace{10pt}i=1..N,\hspace{10pt}j=1..M,\hspace{10pt}k=1..K} \] 

xix_ixi​ ( SETon )نشان‌دهنده موقعیت‌ها و حالت‌های سیستم در سطح میکرو.

• tjt_jtj​ زمان‌های درونی و متغیرهای زمانی سیستم.
• ψk\psi_kψk​ بردارهای حالت کوانتومی-سیستمی که ویژگی‌های دینامیکی و احتمالاتی سیستم را مدل می‌کنند.

این فضا شامل سه نوع اب

 

• x_ixi​ نشان‌دهنده موقعیت‌ها و حالت‌های سیستم در سطح میکرو.
• $t_j$
  

  زمان‌های درونی و متغیرهای زمانی سیستم.

• $\psi_k$
  

  بردارهای حالت کوانتومی-سیستمی که ویژگی‌های دینامیکی و احتمالاتی سیستم را مدل می‌کنند.

این فضا شامل سه نوع ابعاد پایه‌ای است:

1. بعد فیزیکی: مختصات و سرعت‌ها
2. بعد زمانی: زمان‌های چندگانه و نرخ‌های تحول
3. بعد حالت: بردارهای کوانتومی و ویژگی‌های سیستم

---

۲.۲ توپولوژی و هندسه

فضای SETon دارای ویژگی‌های زیر است:

• ناهمگنی (Inhomogeneity): برخی بخش‌ها ممکن است گذارهای سریع داشته باشند.
• گسست‌ها (Discontinuities): نقاطی که مشتقات متغیرها تعریف نمی‌شوند.
• آشوب و فراکتال: رفتار سیستم در مقیاس‌های مختلف، نمایانگر ساختار فراکتالی است.
• متریک کوانتومی-سیستمی: فاصله بین دو حالت سیستم با بردار
  
  $\psi$
  

  تعریف می‌شود:

$$d(\psi_a, \psi_b) = \sqrt{ \langle \psi_a – \psi_b | \psi_a – \psi_b \rangle }$$

---

۳. ریاضیات حاکم بر SETon

۳.۱ بردارهای حالت و فضای هیلبرت

• بردار حالت $\psi$ $\mathrm{<span\; style="font-size:\; 1rem;">\; در\; فضای\; هیلبرت\; </span>}$ $\mathcal{H}$
  

  قرار دارد:

$$\psi \in \mathcal{H} \quad , \quad \langle \psi | \psi \rangle = 1$$

• این بردارها توصیف‌کننده احتمالات وقوع حالات مختلف سیستم هستند.

۳.۲ عملگرها

عملگرها (

$\hat{O}$

) در SETon، نقشی مشابه مکانیک کوانتومی دارند ولی در سطح سیستم‌ها و زمان‌های چندگانه:

$$\hat{O}: \mathcal{H} \rightarrow \mathcal{H}$$

انواع عملگرها

1. عملگر تحول زمانی ($\hat{T}$)

   
   نرخ تغییر بردار حالت بر حسب زمان‌های درونی و بیرونی:

   $$\hat{T}\psi = i \hbar \frac{\partial \psi}{\partial t_j}$$
   
2. عملگر مکان-حالت ($\hat{X}$)
   

   موقعیت سیستم‌ها یا عناصر آن در فضای فیزیکی-سیستمی:

   $$\hat{X}\psi = x_i \psi$$
   
3. عملگر انرژی-سیستم ($\hat{H}$)

   
   انرژی کل سیستم شامل انرژی تعاملی و پویا:

   
   
   
   $$\hat{H}\psi = \sum_i \frac{\hat{P}_i^2}{2m_i} + V(\{x_i\}, t_j) \psi$$
   
4. عملگر گسست (
   
   $\hat{\Delta}$
   

   )
   
   تشخیص نقاط گذار یا آشوب:

   
   
   
   $$\hat{\Delta} \psi = \begin{cases} 0 & \text{در مناطق پیوسته} \\ \infty & \text{در گسست‌ها} \end{cases}$$
   
5. عملگر تعمیم احتمالی (
   
   $\hat{\Omega}$
   

   )
   
   تغییر احتمالات سیستم و توزیع‌های چندزمانه:

   
   
   
   $$\hat{\Omega} \psi = \sum_k \omega_k \psi_k$$
   

---

۳.۳ قواعد ریاضی

• ارتباط عملگرها:

$$[\hat{X}_i, \hat{P}_j] = i \hbar \delta_{ij} \quad , \quad [\hat{T}_j, \hat{H}] = i \hbar \frac{\partial}{\partial t_j} \hat{H}$$

• مقدار مورد انتظار (Expectation Value):

$$\langle \hat{O} \rangle = \langle \psi | \hat{O} | \psi \rangle$$

این مقدار رفتار میانگین سیستم در شرایط کوانتومی-سیستمی را توصیف می‌کند.

---

۴. منطق و اصول حاکم

1. اصل همپوشانی (Superposition Principle):
   
   هر حالت سیستم می‌تواند ترکیب خطی از حالت‌های پایه باشد:
   
   
   $$\psi = \sum_k c_k \psi_k$$
   
2. اصل عدم قطعیت:
   
   مشابه مکانیک کوانتومی، اما برای متغیرهای سیستمی و زمانی:
   
   
   $$\Delta X \Delta P \geq \frac{\hbar}{2}, \quad \Delta t_i \Delta H \geq \frac{\hbar}{2}$$
   
3. اصل تکامل سیستم‌ها:
   
   سیستم‌ها در SETon تحت قوانین دینامیکی عملگرها و گسست‌ها تکامل می‌یابند و گذارهای پیچیده نشان می‌دهند.

---

۵. مثال کاربردی ساده

فرض کنید سیستم دوزمانه‌ای با دو حالت

$\psi_0$

و

$\psi_1$

داریم. عملگر گسست

$\hat{\Delta}$

نقاطی را که تغییر ناگهانی در نرخ تحول رخ می‌دهد تشخیص می‌دهد:

$$\psi(t_1, t_2) = c_0 \psi_0 + c_1 e^{-i \hat{H} t_1 / \hbar} e^{-i \hat{\Omega} t_2 / \hbar} \psi_1$$

مقدار مورد انتظار انرژی سیستم:

$$\langle H \rangle = |c_0|^2 E_0 + |c_1|^2 E_1$$

---

۶. جمع‌بندی

• فضای SETon ترکیبی از ابعاد فیزیکی، زمانی و حالت است.
• عملگرها ابزار اصلی تحلیل تکامل، گسست و آشوب سیستم‌ها هستند.
• منطق کوانتومی-سیستمی همراه با ریاضیات برداری و توپولوژی، چارچوب نظری و تحلیلی برای مطالعه سیستم‌های پیچیده ارائه می‌کند.
• این جزوه پایه‌ای برای توسعه مدل‌ها، شبیه‌سازی‌ها و تمرین‌های عددی در نظریه SETon فراهم می‌کند.

---

ا