فضا، ریاضیات، منطق و فیزیک مکانیک حاکم بر نظریه SET و عملگرها

از /

 

🔹 جزوه مقدماتی فضا و عملگرهای نظریه تحول سیستمی (SET)

بخش ۱: فضای SET — تعریف و ساختار

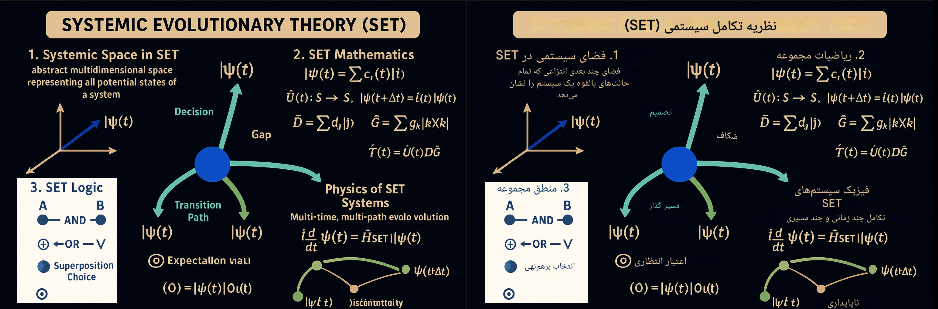
در نظریه تحول سیستمی (SET)، فضا محیطی چندلایه و چندزمانه است که وضعیت سیستم‌ها و گذارهای آن‌ها را تعیین می‌کند.

  • عناصر: نهادهای سیستم
    SiS_i

     

    و زیرسیستم‌ها

    sjs_j

     

  • بردارهای حالت SET:
    ∣Ψ⟩∈S|\Psi\rangle \in \mathcal{S}

     

    که وضعیت کل سیستم را در یک لحظه توصیف می‌کند.

  • فضای SET (
    S\mathcal{S}

     

    ) مشابه فضای هیلبرت کوانتومی، یک فضای برداری با ساختار پیچیده و متغیر در زمان است.

ویژگی‌ها:

  • چندزمانه: شامل زمان‌های محلی و جهانی سیستم‌ها
  • چندسطحی: شامل لایه‌های فیزیکی، اطلاعاتی و تصمیم‌گیری
  • قابل گسست: مناطق با تغییرات ناگهانی و گذارهای سیستمی

بخش ۲: ریاضیات و منطق SET

🔹 بردارهای حالت و ناحیه‌ها

  • هر بردار
    ∣Ψ⟩|\Psi\rangle

     

    شامل اطلاعات زیر است: 

    ∣Ψ⟩=∑i,jci,j∣Si,tj⟩|\Psi\rangle = \sum_{i,j} c_{i,j} |S_i, t_j\rangle

     


  • ci,jc_{i,j}

     

    وزن یا احتمال وقوع یک حالت در زمان

    tjt_j

     

    و نهاد

    SiS_i

     

🔹 ضرب داخلی و اندازه‌گیری

  • ضرب داخلی:
    ⟨Φ∣Ψ⟩\langle \Phi | \Psi \rangle

     

    اندازه همبستگی بین دو حالت SET را می‌دهد.

  • مقدار انتظار یک کمیت سیستم: 
    ⟨A⟩=⟨Ψ∣A^∣Ψ⟩\langle A \rangle = \langle \Psi | \hat{A} | \Psi \rangle

     

🔹 منطق جبری

  • جمع:
    (A^+B^)∣Ψ⟩=A^∣Ψ⟩+B^∣Ψ⟩(\hat{A} + \hat{B})|\Psi\rangle = \hat{A}|\Psi\rangle + \hat{B}|\Psi\rangle

     

  • ضرب:
    (A^B^)∣Ψ⟩=A^(B^∣Ψ⟩)(\hat{A}\hat{B})|\Psi\rangle = \hat{A}(\hat{B}|\Psi\rangle)

     

  • جابجایی:
    [A^,B^]=A^B^−B^A^[\hat{A}, \hat{B}] = \hat{A}\hat{B} – \hat{B}\hat{A}

     

در SET، جابجایی عملگرها نمایانگر تداخل و محدودیت همزمان تصمیم‌ها و گذارها است.

بخش ۳: عملگرهای SET — مفهوم و نقش

🔹 تعریف عملگر

عملگر

A^\hat{A}

در SET نماینده اثر یک نیرو، تصمیم یا قانون حاکم بر زیرسیستم‌ها است:

 

A^∣Ψ⟩=∣Ψ′⟩\hat{A} |\Psi\rangle = |\Psi’\rangle

 

🔹 انواع عملگرها

  1. عملگر تحول زمانی
    T^Δt\hat{T}_{\Delta t}

     

    • تکامل حالت سیستم در یک بازه زمانی:

      T^Δt∣Ψ(t)⟩=∣Ψ(t+Δt)⟩\hat{T}_{\Delta t} |\Psi(t)\rangle = |\Psi(t+\Delta t)\rangle

       

  2. عملگر گسست
    G^\hat{G}

     

    • اعمال تغییر ناگهانی (ناحیه آشوب):

      G^∣Ψ⟩=∣Ψ′⟩گسسته\hat{G}|\Psi\rangle = |\Psi’\rangle_{\text{گسسته}}

       

  3. عملگر تصمیم/کنش
    D^i\hat{D}_i

     

    • تغییر وضعیت زیرسیستم‌ها با توجه به ورودی یا قانون انتخاب:

      D^i∣Si⟩=∣Si′⟩\hat{D}_i |S_i\rangle = |S_i’\rangle

       

  4. عملگر همبستگی
    C^ij\hat{C}_{ij}

     

    • میزان تأثیر متقابل بین دو زیرسیستم:

      C^ij∣Si,Sj⟩=cij∣Si,Sj⟩\hat{C}_{ij} |S_i, S_j\rangle = c_{ij} |S_i, S_j\rangle

       

بخش ۴: روابط و جبر عملگرهای SET

  • جمع و ضرب عملگرها: همانند کوانتوم
  • جابجایی عملگرها:

 

[A^,B^]≠0  ⟹  محدودیتهمزمانوتداخلسیستم‌ها[\hat{A}, \hat{B}] \neq 0 \implies محدودیت همزمان و تداخل سیستم‌ها

 

  • عملگرهای همزمان: اگر
    [A^,B^]=0[\hat{A}, \hat{B}] = 0

     

    ، گذارها و تصمیم‌ها می‌توانند همزمان رخ دهند

🔹 تقارن‌ها در SET

  • تقارن زمانی:
    [H^SET,T^Δt]=0[\hat{H}_{SET}, \hat{T}_{\Delta t}] = 0

     

    → سیستم پایسته در زمان

  • تقارن مکانی/فضایی:
    P^SET∣Ψ⟩=∣Ψmirror⟩\hat{P}_{SET} |\Psi\rangle = |\Psi_{\text{mirror}}\rangle

     

  • تقارن تصمیم: عملگرهای همزمان تصمیم مستقل از یکدیگر

بخش ۵: جدول عملگرهای SET

نوع عملگر نماد عملکرد دامنه اثر ویژگی‌ها روابط جابجایی
تحول زمانی

T^Δt\hat{T}_{\Delta t}

 

 تکامل حالت کل فضای

S\mathcal{S}

 

 پایستگی زمانی —
گسست

G^\hat{G}

 

 تغییر ناگهانی نواحی آشوب غیرخطی، ناپایدار

[G^,T^Δt]≠0[\hat{G}, \hat{T}_{\Delta t}] \neq 0

 
تصمیم

D^i\hat{D}_i

 

 تغییر وضعیت زیرسیستم

SiS_i

 

 وابسته به ورودی —
همبستگی

C^ij\hat{C}_{ij}

 

 اثر متقابل

Si,SjS_i, S_j

 

 خطی یا غیرخطی —
شمارنده تحول

N^SET\hat{N}_{SET}

 

 تعداد گذارهای موفق کل فضای

S\mathcal{S}

 

 هرمیتی

[N^SET,D^i]=−D^i[\hat{N}_{SET}, \hat{D}_i] = -\hat{D}_i

 

بخش ۶: مقدار انتظار و تحلیل

مقدار انتظار یک کمیت در SET مشابه کوانتوم است:

 

⟨A⟩=⟨Ψ∣A^∣Ψ⟩\langle A \rangle = \langle \Psi | \hat{A} | \Psi \rangle

 

  • نشان‌دهنده میانگین اثر یا نتیجه یک قانون یا تصمیم در فضای سیستم
  • به ویژه برای تحلیل گذارها، آشوب و پایداری سیستم‌ها کاربرد دارد

بخش ۷: مثال کاربردی SET

فرض کنیم زیرسیستم

SiS_i

تحت تصمیم

D^i\hat{D}_i

و گسست

G^\hat{G}

قرار گیرد:

 

∣Ψ′⟩=G^D^i∣Ψ⟩|\Psi’\rangle = \hat{G}\hat{D}_i |\Psi\rangle

 

  • این نشان می‌دهد که تصمیم و گسست ترکیبی، مسیر تحول کل سیستم را تغییر می‌دهد
  • اگر
    [D^i,G^]≠0[\hat{D}_i, \hat{G}] \neq 0

     

    ، اثر تصمیم وابسته به وقوع گسست است

بخش ۸: جمع‌بندی

  • فضای SET: چندزمانه، چندلایه و شامل نواحی پایدار و آشوب
  • بردارهای حالت: توصیف وضعیت کل سیستم و زیرسیستم‌ها
  • عملگرها: نماینده قوانین، تصمیم‌ها، گسست‌ها و همبستگی‌ها
  • جبر و روابط عملگرها: تحلیل همزمانی، تداخل و محدودیت‌ها
  • مقدار انتظار: میانگین اثر عملگرها و تحلیل گذارهای سیستم

بخش ۹: منابع پیشنهادی برای مطالعه

  1. نظریه تحول سیستمی (SET) — مقالات و منابع اولیه TacZi (فرهاد تقوائی)
  2. Mathematical Methods in Physics — Arfken & Weber (برای فضای برداری و عملگرها)
  3. Complex Systems and Chaos Theory — Strogatz

 

دیدگاه‌ خود را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *

پیمایش به بالا